Kvantumszámítógép - kevés (hipotetikus) tudományos vívmányról írtak annyi érdekességet és hordtak össze annyi zöldséget, mint a kvantumszámítógépről. A valaha volt legnagyobb informatikai áttörés, avagy humbug, a modern alkimisták aranya? Mindenki derítse ki maga, itt igyekszünk csak a konkrétumokat elészámlálni. Dilbert mindenestre már döntött. 

Forrás: wikipedia

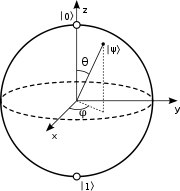
Tudvalevő, hogy a klasszikus digitális számítógépek adategysége a (klasszikus) bit, mely két értéket vehet fel: 0-t, illetve 1-et. A kvantumszámítógép kvantumbitje, amit qbitnek is szoktak rövidíteni, ezzel szemben végtelen sok értéket vehet fel: a 0 és 1 állapotok tetszőleges komplex szuperpozícióját. Vagy, ha képzeletben a Földgömbre vetítjük a problémát, akkor azt mondhatjuk, hogy míg a klasszikus bit vagy az Északi Sark, vagy a Déli Sark értéket veheti fel kizárólagosan, addig a kvantumbit a Földgömb tetszőleges pontjára mutathat, ugye mekkora előrelépés? — mondja valahány botcsinálta bociszemű népművelő. Ez minden? — kérdezhetné akárhány villamosmérnök, s a zsebében véletlenül kinyílt bicskájával tűntetőleg piszkálni kezdené a körmét. — Hiszen ezt bármilyen analóg számítógép utánatok csinálja, fillérekért! Jöjjön csak közelebb, Safranek!

Forrás: Iain Stewart's homepage

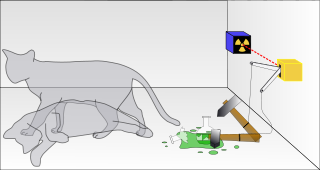
Nem, nem ennyi. Küldjük szépen el a bociszeműt, mondjon máshol okosakat, a vebkettőről például, és lássunk komolyan neki a kérdés boncolgatásának. Ha komplex problémák megoldásáról van szó, a kvantumszámítógép olyan forrásból is erőt meríthet, mely klasszikusan értelmezhetetlen: a kvantumállapotok összefonódottságából. Az meg mi fán terem? Nos, a válaszhoz visszamegyünk a fizika történetének legnépszerűbb és legboldogtalanabb háziállatához, Schrödinger macskájához. Képzeljük el a következőt: fogunk egy dobozt, ebbe elhelyezünk egy kis radioaktív anyagdarabkát, pont olyat és annyit, hogy egy perc alatt épp 50%-nyi valószínűséggel bocsásson ki egy alfa-részecskét. Nomármost, a radioaktív bomlás tipikus kvantummechanikai folyamat: nem determinisztikus. A legpontosabb számítás is csak annyi információt szolgáltathat, hogy az anyag egy atommagja adott idő alatt mekkora valószínűséggel bomlik, de hogy a bomlás valóban megtörténik-e, az véletlenszerű és megjósolhatatlan. Elhelyezünk továbbá egy alfa-detektort is a dobozban, ami a bomlás megtörténtét elektromos impulzussá alakítja. Ez az impulzus kinyit egy méregfiolát, s a dobozba tuszkolt cica szomorú véget ér. Ha megtörtént a radioaktív bomlás. Ha nem, akkor nem.

Forrás: wikipedia

Még egy fontos dolog: a detektort pontosan egy percre kapcsolja be egy időzítő szerkezet, de előtte a dobozt lezárjuk. De nem csak úgy tessék-lássék módon, hanem rendesen. Nem lehet leskelődni a kísérlet közben. Nincs olyan, hogy a CIA egy kémegeret csempészett be a dobozba, aki rádión közvetít (mellesleg, jó kis küldetés lenne ez egy egérnek: radioktív anyaggal, méreggel és macskával bezárkózni). Szóval nincs ilyesmi. Olyan dobozt eszkábálunk, hogy természeti törvény tiltja az idő előtti felnyitását. Komolyan, máshogy nem megy: természet Ősanyánk nem hisz különben nekünk, hiába esküdözünk, megmakacsolja magát, és a kísérlet nem működik. Ezért aztán felesleges is az állatvédőkhöz rohanni: a kísérletet nem végezték el, nem készülnek elvégezni, mert lehetetlen. Csupán gondolatkísérlet. Szóval, mit tippelünk, milyen állapotban lesz a cica az egy perc letelte után? A radioaktív mag vagy bomlott, vagy sem, lehetetlen megmondani, amíg rá nem nézünk. Fél valószínűséggel elbomlott, fél valószínűséggel nem. A detektor ennek megfelelően jelzett, vagy sem, s a cirmi is fél valószínűséggel elszenderült, fél valószínűséggel nem: állapotfüggvénye az élő és halott állapot szuperpoziciója. Mikor kinyitom a dobozt, és rápillantok (mérést végzek), akkor „ugrik” véletlenszerűen egyik vagy másik állapotba. Na, ez marhaság - mondta Schrödinger, tudniillik ő pont a gondolatmenet abszurd voltára igyekezett ezzel az extrém pédával rávilágítani. Macskával marhaság — a mikrovilág objektumaival sziklaszilárd kísérleti tény. Mert a mikrovilágban lehet olyan dobozt találni, aminek a felnyitását természettörvény tiltja. De ez egy másik történet lenne.

 De térjünk csak vissza az eredeti gondolatkísérlethez! Milyen állapotban volt a cica a felnyitás előtt? Nem tudjuk, hisz épp azért nyitottuk fel, hogy kiderítsük. És az atommag? Azt se tudjuk. Egyikről sem tudunk semmit — no, de ez már nem igaz! Tudjuk, hogy nincs olyan kimenetel, hogy az atommag nem bomlott el, de a cica mégis elpusztult. De olyan sincs, hogy a cica él, viszont az atommag elbomlott. A két objektum állapota nem független egymástól. Sorsuk összefonódott. Ha az egyikkel történik valami, a másikkal is fog. 

 Ugyanez az összefonódottság adja a kvantumszámítógép hihetetlen fölényét klasszikus társa felett:  a kvantumszámítógépben a qbitek összefonódott állapotban vannak. Ha egyiken műveletet végzek, a többi állapota is megváltozik. Azonnal. Tökéletes párhuzamosítás. Node mire jó ez? És hogyan lehetne ilyen derék eszközt fabrikálni? Éppen ezzekkel a kérdésekkel fogunk legközelebb foglalkozni.